信号滤波

大约 14 分钟低通滤波高通滤波带通滤波带阻滤波卡尔曼滤波

1. 低通滤波

概念与原理介绍

低通滤波是一种信号处理技术，通过去除信号中高频成分，保留较低频的成分，以实现信号平滑和去噪的目的。低通滤波器的原理是在给定的截止频率以下传递信号的成分，并衰减高于截止频率的成分。这可以通过设计合适的滤波器来实现，如巴特沃斯滤波器、滑动平均滤波器等。低通滤波器的传递函数可以表示为 H_LP(ω)，其中 ω 是频率。具体的滤波器设计方法可以根据不同的滤波器类型而异。该方法可以运用于以下各个方面，如

音频处理中的去除高频噪声和杂音。
图像处理中的平滑和去除高频细节。
生物信号处理中的滤除肌电干扰等。
传感器信号处理中的去除高频振动和干扰。

Python实现

如果依赖库未安装，那就需要先对本章节所用到的python依赖库进行下载安装：

pip install -i https://pypi.tuna.tsinghua.edu.cn/simple numpy
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple scipy
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple matplotlib

下面是一个低频滤波的Python实现示例，包括生成信号和使用低通滤波器进行滤波，并使用Matplotlib库展示结果。

import numpy as np
from scipy import signal
import matplotlib.pyplot as plt

# 生成信号
fs1 = 1000  # 采样频率
t = np.linspace(0, 1, fs1, endpoint=False)  # 时间向量
f = 5  # 信号频率
data1 = np.sin(2 * np.pi * f * t) + np.sin(2 * np.pi * 35 * t)  # 正弦信号


# 设计低通滤波器
def lowpass_filter(data, cutoff_freq, fs):
    b, a = signal.butter(4, cutoff_freq / (fs / 2), 'low')
    # 使用滤波器进行滤波
    filtered_signal = signal.filtfilt(b, a, data)
    return filtered_signal


cutoff_freq1 = 10  # 截止频率
res = lowpass_filter(data1, cutoff_freq1, fs1)

# 绘制原始信号和滤波后的信号
plt.figure(figsize=(10, 5))
plt.subplot(2, 1, 1)
plt.plot(t, data1)
plt.title('Original Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')

plt.subplot(2, 1, 2)
plt.plot(t, res)
plt.title('Filtered Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')

plt.tight_layout()
plt.show()

以上示例代码中，首先生成了一个频率为5Hz的正弦信号，然后使用signal.butter函数设计了一个4阶低通滤波器，截止频率设置为10Hz。接下来，使用signal.filtfilt函数对生成的信号应用低通滤波器进行滤波。最后，使用Matplotlib库绘制了原始信号和滤波后的信号的时域波形图。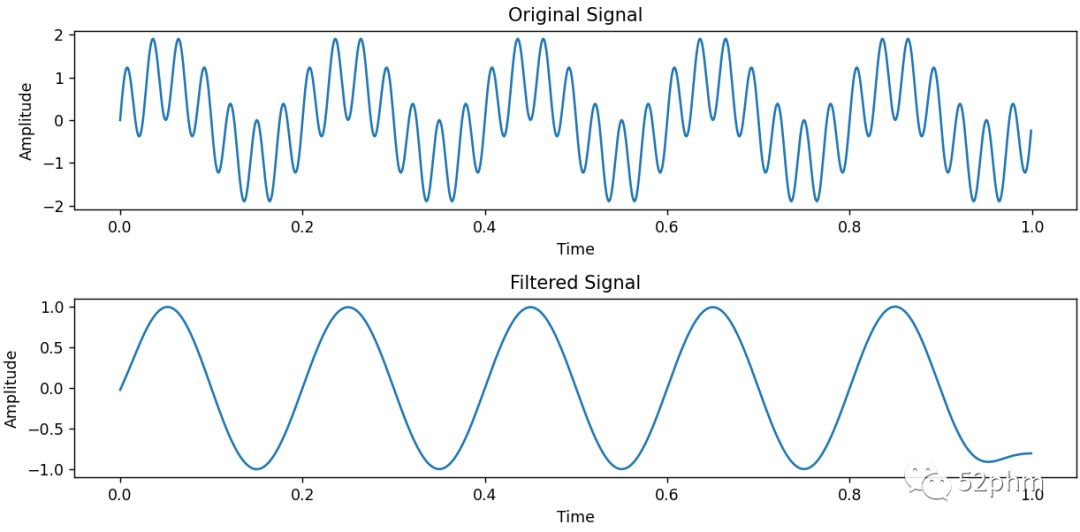运行该示例代码可以展示原始信号和经过低通滤波后的信号的波形图，以直观地展示低频滤波的效果。

总结

低通滤波可以去除信号中的高频噪声和干扰，提高信号的质量和可读性。
低通滤波可以平滑信号，去除快速变化的成分，突出信号的趋势和低频特征。
低通滤波在频域上起到了限制频率范围的作用，使得信号能够更好地适应特定的应用需求。

2. 高通滤波

概念与原理介绍

高通滤波是一种信号处理技术，通过去除信号中低频成分，保留较高频的成分，以实现突出细节和去除趋势的目的。高通滤波器的原理是在给定的截止频率以上传递信号的成分，并衰减低于截止频率的成分。常见的高通滤波器包括巴特沃斯滤波器、理想滤波器等。高通滤波器的传递函数可以表示为 H_HP(ω)，其中 ω 是频率。具体的滤波器设计方法可以根据不同的滤波器类型而异。该方法可以应用于以下各个方面，如：

图像处理中的边缘检测和纹理分析。
音频处理中的语音识别和音乐分析。
传感器信号处理中的检测快速变化和瞬态特征。

Python实现

如果依赖库未安装，那就需要先对本章节所用到的python依赖库进行下载安装：

pip install -i https://pypi.tuna.tsinghua.edu.cn/simple numpy
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple scipy
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple matplotlib

以下是一个以函数形式实现高频滤波的Python代码示例，包括生成信号和使用高通滤波器进行滤波，并使用Matplotlib库展示结果：

import numpy as np
from scipy import signal
import matplotlib.pyplot as plt


def highpass_filter(data, cutoff_freq, fs):
    # 设计高通滤波器
    b, a = signal.butter(4, cutoff_freq / (fs / 2), 'high')
    # 使用滤波器进行滤波
    filtered_signal = signal.filtfilt(b, a, data)
    return filtered_signal


# 生成信号
fs = 1000  # 采样频率
t = np.linspace(0, 1, fs, endpoint=False)  # 时间向量
f = 50  # 信号频率
data = np.sin(2 * np.pi * f * t)  # 正弦信号

# 设定截止频率
cutoff_freq = 30  # 截止频率

# 使用高通滤波器进行滤波
filtered_signal = highpass_filter(data, cutoff_freq, fs)

# 绘制原始信号和滤波后的信号
plt.figure(figsize=(10, 5))
plt.subplot(2, 1, 1)
plt.plot(t, data)
plt.title('Original Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')

plt.subplot(2, 1, 2)
plt.plot(t, filtered_signal)
plt.title('Filtered Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')

plt.tight_layout()
plt.show()

在以上示例代码中，首先定义了一个高通滤波器的函数highpass_filter，通过使用signal.butter函数设计了一个4阶高通滤波器，并使用signal.filtfilt函数对输入信号进行滤波。然后，生成了一个频率为50Hz的正弦信号，设定了截止频率为30Hz。最后，使用Matplotlib库绘制了原始信号和滤波后的信号的时域波形图。运行该示例代码可以展示原始信号和经过高频滤波后的信号的波形图，以直观地展示高频滤波的效果。

总结

高通滤波可以去除信号中的低频成分和趋势，突出信号中的细节和高频特征。
高通滤波可以增强信号的边缘和细微变化，提高信号的清晰度和辨识度。
高通滤波对于特定应用中只关注高频部分的情况非常有用，例如语音处理中的语调分析和音调识别。

3. 带通滤波

概念与原理介绍

带通滤波是一种信号处理技术，通过选择特定的频率范围，使该范围内的信号成分通过，而抑制其他频率范围的信号成分。

带通滤波器的原理是在给定的频率范围内传递信号的成分，并在该范围外衰减信号的成分。常见的带通滤波器包括巴特沃斯滤波器、椭圆滤波器等。带通滤波器的传递函数可以表示为 H_BP(ω)，其中 ω 是频率。具体的滤波器设计方法可以根据不同的滤波器类型而异。

该方法可以应用于以下各个方面，如：

生物信号处理中的心电图（ECG）分析。
无线通信系统中的信号调制和解调。
音频处理中的音乐频谱分析。

Python实现

如果依赖库未安装，那就需要先对本章节所用到的python依赖库进行下载安装：

pip install -i https://pypi.tuna.tsinghua.edu.cn/simple numpy
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple scipy
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple matplotlib

以下是一个以函数形式实现带通滤波的Python代码示例，包括生成信号和使用带通滤波器进行滤波，并使用Matplotlib库展示结果：

import numpy as np
from scipy import signal
import matplotlib.pyplot as plt


def bandpass_filter(data, low_cutoff_freq, high_cutoff_freq, fs):
    # 设计带通滤波器
    b, a = signal.butter(4, [low_cutoff_freq / (fs / 2), high_cutoff_freq / (fs / 2)], 'bandpass')

    # 使用滤波器进行滤波
    filtered_signal = signal.filtfilt(b, a, data)
    return filtered_signal


# 生成信号
fs = 1000  # 采样频率
t = np.linspace(0, 1, fs, endpoint=False)  # 时间向量
f = 50  # 信号频率
data = np.sin(2 * np.pi * f * t)  # 正弦信号

# 设定带通滤波器的截止频率
low_cutoff_freq = 30  # 低频截止频率
high_cutoff_freq = 70  # 高频截止频率

# 使用带通滤波器进行滤波
filtered_signal = bandpass_filter(data, low_cutoff_freq, high_cutoff_freq, fs)

# 绘制原始信号和滤波后的信号
plt.figure(figsize=(10, 5))
plt.subplot(2, 1, 1)
plt.plot(t, data)
plt.title('Original Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')

plt.subplot(2, 1, 2)
plt.plot(t, filtered_signal)
plt.title('Filtered Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')

plt.tight_layout()
plt.show()

在以上示例代码中，首先定义了一个带通滤波器的函数bandpass_filter，通过使用signal.butter函数设计了一个4阶带通滤波器，并使用signal.filtfilt函数对输入信号进行滤波。然后，生成了一个频率为50Hz的正弦信号，并设定了带通滤波器的低频截止频率和高频截止频率为30Hz和70Hz。最后，使用Matplotlib库绘制了原始信号和滤波后的信号的时域波形图。运行该示例代码可以展示原始信号和经过带通滤波后的信号的波形图，以直观地展示带通滤波的效果。

总结

带通滤波可以选择感兴趣的频率范围，保留该范围内的信号成分，抑制其他频率范围的干扰。
带通滤波对于关注特定频率范围内的信号分析和处理非常有用，例如心电信号中特定频率范围内的心跳信息。

4. 带阻滤波

概述与原理介绍

带阻滤波是一种信号处理技术，通过选择特定的频率范围，使该范围内的信号成分被抑制，而其他频率范围的信号成分通过。

带阻滤波器的原理是在给定的频率范围内衰减信号的成分，并在该范围外传递信号的成分。常见的带阻滤波器包括巴特沃斯滤波器、椭圆滤波器等。

带阻滤波器的传递函数可以表示为 H_BS(ω)，其中 ω 是频率。具体的滤波器设计方法可以根据不同的滤波器类型而异。

另外可以应用在以下方面，如：

电力系统中的电源频率干扰去除。
语音信号处理中的去除特定频率范围的噪声。
音频处理中的音频效果器设计，如去除特定频率的回声。

Python实现

如果依赖库未安装，那就需要先对本章节所用到的python依赖库进行下载安装：

pip install -i https://pypi.tuna.tsinghua.edu.cn/simple numpy
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple scipy
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple matplotlib

以下是一个以函数形式实现带阻滤波的Python代码示例，包括生成信号和使用带阻滤波器进行滤波，并使用Matplotlib库展示结果：


import numpy as np
from scipy import signal
import matplotlib.pyplot as plt


def bandstop_filter(data, low_cutoff_freq, high_cutoff_freq, fs):
    # 设计带阻滤波器
    b, a = signal.butter(4, [low_cutoff_freq / (fs / 2), high_cutoff_freq / (fs / 2)], 'bandstop')

    # 使用滤波器进行滤波
    filtered_signal = signal.filtfilt(b, a, data)
    return filtered_signal


# 生成信号
fs = 1000  # 采样频率
t = np.linspace(0, 1, fs, endpoint=False)  # 时间向量
f = 50  # 信号频率
data = np.sin(2 * np.pi * f * t)  # 正弦信号

# 设定带阻滤波器的截止频率
low_cutoff_freq = 40  # 低频截止频率
high_cutoff_freq = 60  # 高频截止频率

# 使用带阻滤波器进行滤波
filtered_signal = bandstop_filter(data, low_cutoff_freq, high_cutoff_freq, fs)

# 绘制原始信号和滤波后的信号
plt.figure(figsize=(10, 5))
plt.subplot(2, 1, 1)
plt.plot(t, data)
plt.title('Original Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')

plt.subplot(2, 1, 2)
plt.plot(t, filtered_signal)
plt.title('Filtered Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')

plt.tight_layout()
plt.show()

在以上示例代码中，首先定义了一个带阻滤波器的函数bandstop_filter，通过使用signal.butter函数设计了一个4阶带阻滤波器，并使用signal.filtfilt函数对输入信号进行滤波。然后，生成了一个频率为50Hz的正弦信号，并设定了带阻滤波器的低频截止频率和高频截止频率为40Hz和60Hz。最后，使用Matplotlib库绘制了原始信号和滤波后的信号的时域波形图。运行该示例代码可以展示原始信号和经过带阻滤波后的信号的波形图，以直观地展示带阻滤波的效果。

总结

带阻滤波可以选择特定频率范围以外的信号成分通过，抑制该范围内的干扰。
带阻滤波对于去除特定频率范围内的噪声和干扰非常有用，例如电力系统中的50Hz或60Hz电源干扰。

5、卡尔曼滤波

概念与原理介绍

卡尔曼滤波是一种基于状态空间模型的最优滤波算法。它通过对系统的状态进行预测和校正，结合观测数据和系统模型，实现对未知信号的估计和滤波。卡尔曼滤波器基于线性系统假设，通过迭代的方式对系统的状态进行预测和校正，使得估计值更接近真实值。它利用过去的状态估计和观测数据，通过最小均方误差准则来计算状态的最优估计。公式卡尔曼滤波器的公式包括状态预测和状态更新两个步骤。状态预测根据系统模型预测下一时刻的状态，状态更新利用观测数据对预测值进行校正，并更新状态估计。

状态预测：
- 状态预测方程：x(k|k-1) = F * x(k-1|k-1) + B * u(k)
- 误差协方差预测方程：P(k|k-1) = F * P(k-1|k-1) * F^T + Q
状态更新：
- 卡尔曼增益方程：K(k) = P(k|k-1) * H^T * (H * P(k|k-1) * H^T + R)^(-1)
- 状态更新方程：x(k|k) = x(k|k-1) + K(k) * (z(k) - H * x(k|k-1))
- 误差协方差更新方程：P(k|k) = (I - K(k) * H) * P(k|k-1)

卡尔曼滤波广泛应用于信号处理、控制系统、导航定位、目标跟踪等领域。它适用于估计具有动态变化和噪声的系统状态，并能够提供准确的状态估计和滤波结果。

Python实现

如果依赖库未安装，那就需要先对本章节所用到的python依赖库进行下载安装：

pip install -i https://pypi.tuna.tsinghua.edu.cn/simple numpy
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple filterpy
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple matplotlib

在Python中，可以使用filterpy库来实现卡尔曼滤波。以下是一个简单的示例：


from filterpy.kalman import KalmanFilter
import numpy as np
import matplotlib.pyplot as plt


def kalman_filter(data):
    # 初始化Kalman滤波器
    kf = KalmanFilter(dim_x=2, dim_z=1)

    # 设置状态转移矩阵
    kf.F = np.array([[1., 1.],
                     [0., 1.]])

    # 设置观测矩阵
    kf.H = np.array([[1., 0.]])

    # 设置过程噪声协方差矩阵
    kf.Q = np.array([[0.01, 0.],
                     [0., 0.01]])

    # 设置观测噪声协方差矩阵
    kf.R = np.array([[0.1]])

    # 初始化状态向量和协方差矩阵
    kf.x = np.array([0., 0.])
    kf.P = np.eye(2)

    filtered_signal = []

    for measurement in data:
        # 预测下一时刻的状态和协方差矩阵
        kf.predict()

        # 根据观测值对预测值进行校正
        kf.update(measurement)

        # 获取滤波后的状态估计
        filtered_signal.append(kf.x[0])

    return filtered_signal


# 生成带噪声的信号
t = np.linspace(0, 1, 100)
data = np.sin(2 * np.pi * 5 * t) + np.random.normal(0, 0.1, 100)

# 进行卡尔曼滤波
filtered_signal = kalman_filter(data)

# 绘制原始信号和滤波后的信号
plt.figure(figsize=(8, 6))
plt.plot(t, data, label='Original Signal')
plt.plot(t, filtered_signal, label='Filtered Signal')
plt.legend()
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.title('Kalman Filter')
plt.grid(True)
plt.show()

该函数接受一个信号作为输入，并返回经过卡尔曼滤波后的信号。在函数内部，我们首先初始化一个KalmanFilter对象，并设置状态转移矩阵F、观测矩阵H、过程噪声协方差矩阵Q和观测噪声协方差矩阵R。然后，我们通过预测和校正的过程对每个观测值进行滤波，最后将滤波后的状态估计添加到filtered_signal列表中并返回。

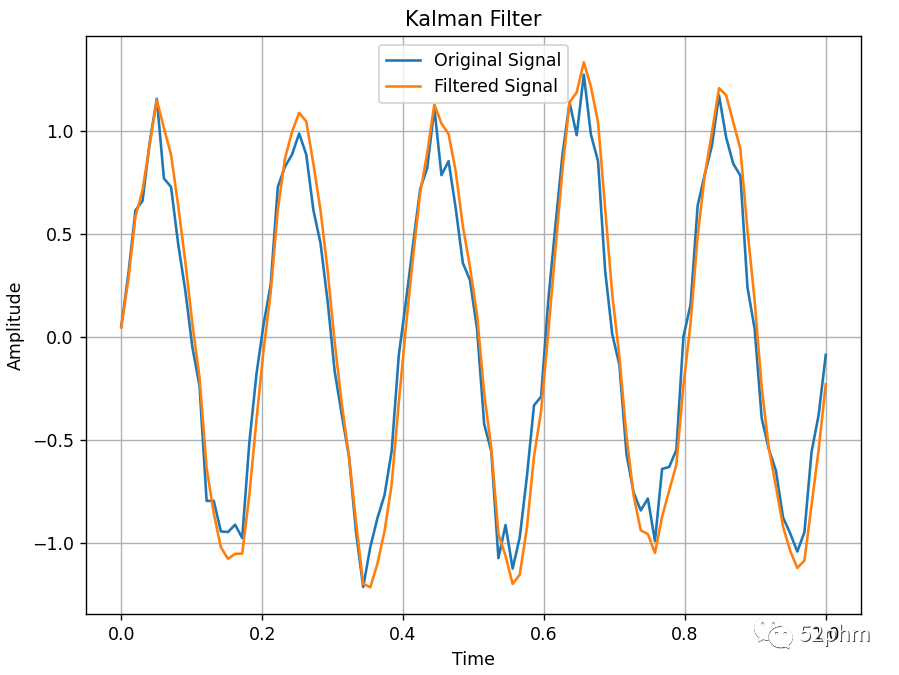
上述代码中，我们生成一个带噪声的信号，然后调用kalman_filter函数对信号进行卡尔曼滤波，并使用Matplotlib库将原始信号和滤波后的信号绘制在同一图像上进行对比。

总结

卡尔曼滤波器能够对系统的状态进行估计和滤波，具有优良的估计性能和递归更新性质。它可以在观测数据有噪声的情况下，准确地估计系统的状态，并能够根据系统模型和观测数据的权重自适应地调整滤波效果。

信号滤波

# 1. 低通滤波

# 概念与原理介绍

# Python实现

# 总结

# 2. 高通滤波

# 概念与原理介绍

# Python实现

# 总结

# 3. 带通滤波

# 概念与原理介绍

# Python实现

# 总结

# 4. 带阻滤波

# 概述与原理介绍

# Python实现

# 总结

# 5、卡尔曼滤波

# 概念与原理介绍

# Python实现

# 总结

1. 低通滤波

概念与原理介绍

Python实现

总结

2. 高通滤波

概念与原理介绍

Python实现

总结

3. 带通滤波

概念与原理介绍

Python实现

总结

4. 带阻滤波

概述与原理介绍

Python实现

总结

5、卡尔曼滤波

概念与原理介绍

Python实现

总结