振动分析基础知识

1、振动的概念

振动是指物体在平衡位置附近围绕平衡位置作周期性变化的现象。在机械系统中，振动通常是由不平衡驱动力、弹性元件以及阻尼元件等引起的。振动分析是一种用于检测和诊断设备故障的技术，能够帮助工程师发现设备的潜在问题。

2、振动的三要素

振动的三要素包括：

• 振幅（Amplitude）：振动的最大偏离程度，是评判机器运转状态优劣的主要指标，用字母A表示，通常用来表征振动的强度，振幅越大，振动越强烈。
• 频率（Frequency）：频率表示振动在单位时间内完成的周期数，通常以赫兹（Hz）为单位。频率反映了振动的快慢。
• 相位（Phase）：相位表示相对于参考点的振动的位置关系，用角度或者时间表示。相位关系可以帮助我们识别振动源的位置和方向。

3、振动在故障诊断领域的作用

振动分析在故障诊断领域具有重要作用，主要体现在以下几点：

• 振动数据可以反映设备的运行状态，包括设备的健康状况和工作负荷；
• 通过对振动数据进行分析，可识别设备中的不平衡、轴承故障、齿轮故障等问题；
• 振动分析可以在设备出现故障前进行预警，降低设备的维修成本和停机时间。

4、振动分析的应用场景

振动分析主要使用方法包括：

• 数据采集：使用传感器（如加速度传感器）获取设备的振动数据；
• 信号处理：对采集到的振动数据进行滤波、平滑等预处理操作；
• 特征提取：从处理后的振动数据中提取有用的特征，如频谱、时域特征等；
• 故障诊断：根据提取的特征，运用专家知识或机器学习算法识别设备故障。

应用场景包括：

• 旋转设备（如电机、泵、轴承等）的故障检测；
• 风力发电机组的故障诊断；
• 铁路轴承故障检测；
• 航空发动机故障诊断等。

5、简谐运动

下面将通过简谐运动来举例介绍振动三要素。简谐运动是指物体沿着某个轴或面做周期性往复运动，且受到一个恢复力的作用。简谐运动的一个重要特点是，所受的恢复力与物体运动的位移成正比，方向与运动方向相反。简谐运动也可以用振幅、频率和相位来描述。例如，弹簧振子就是一种简谐运动。简谐运动在力学、电学、声学、光学等领域都有重要的应用。简谐运动是物体在弹性力作用下作周期性运动的一种基本形式。设物体的位移函数为：

$x(t) = A \cdot \cos(2\pi ft + \phi)$

其中，$A$ 表示振幅，$f$ 表示频率，$t$ 表示时间，$\phi$ 表示相位。

假设一个简谐运动的振动参数如下：

• 振幅：$A = 5\text{mm}$
• 频率：$f = 10\text{Hz}$
• 相位：$\phi = \frac{\pi}{6}$

则物体的位移函数为：

$x(t) = 5 \cdot \cos(20\pi t +\frac{\pi}{6})$

import numpy as np
import matplotlib.pyplot as plt


t=np.arange(1024)*(1/1024)
x=5*np.cos(20*np.pi*t+(np.pi/6))
plt.plot(t, x)
plt.xlabel('t')
plt.ylabel('Amp')
plt.show()

振动简谐运动

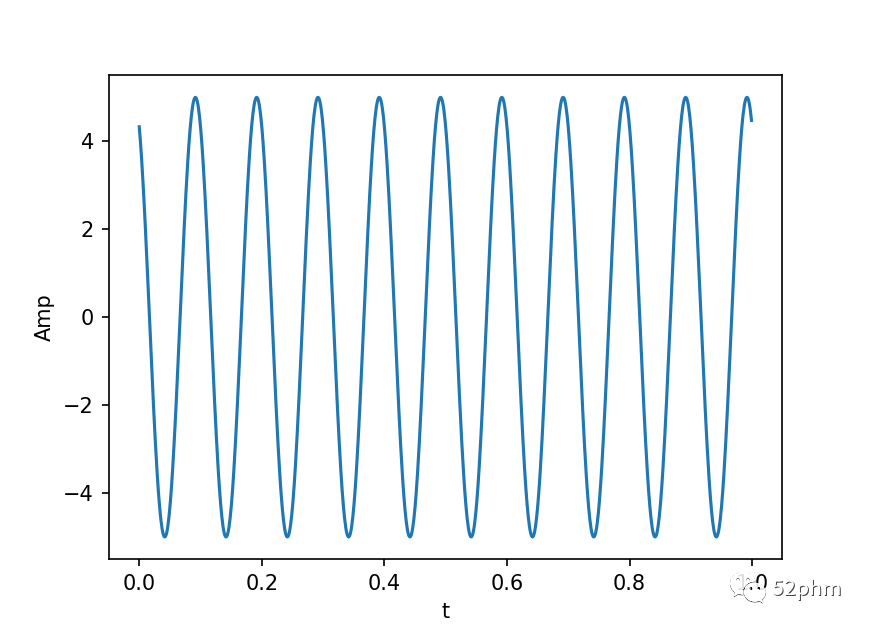
在此简谐运动示例中：

• 振幅为 $5\text{mm}$，表示物体在振动过程中离平衡位置的最大距离为 $5\text{mm}$；
• 频率为 $10\text{Hz}$，表示物体在 $1\text{s}$ 内完成 $10$ 个完整的振动周期；
• 相位为 $\frac{\pi}{6}$，表示物体在时间 $t=0$ 时，位移与参考位移之间的相位差为 $30^\circ$。

6、常用振动指标的概述

正弦函数是一种标准的周期性函数，它可以用于描述许多物理现象中的振动。在振动分析中，我们经常使用正弦函数来表示振动信号，因为它们具有清晰的周期性和可预测的性质。以下是正弦函数关于振动指标的公式和概述：

1. 均方根 (RMS)：均方根是一个振动信号的有效值。它可以通过信号的平方平均值再开根号得到。

• 公式：RMS = sqrt((1/N) * Σ(x^2))
• 其中，N是样本数，x是振动信号。

2. 峰值 (Peak)：峰值是振动信号中的最大值。

• 公式：Peak = max(x)

3. 峰峰值 (Peak-to-Peak)：峰峰值是振动信号中最大值和最小值之间的差值。

• 公式：Peak-to-Peak = max(x) - min(x)

4. 平均值 (Mean)：平均值是振动信号的平均值。

• 公式：Mean = (1/N) * Σ(x)

这些振动指标在振动分析中非常有用。例如，RMS可以用于评估信号的振动能量，即评估振动的破环能力，峰值可以用于检测信号中的异常点或评估机器瞬间承受冲击的振动量大小，峰峰值可以用于检测机器振动位移量的大小，而平均值可以用于分析信号的基本趋势。